النسب المثلثية ومقلوباتها

تمهيد:

ماهي النسب المثلثية ؟  ولماذا أطلق عليهاهذا الاسم؟

نعلم ان النسبة في أبسط صورها هي مقارنة بين مقدارين مثلاً النسبة بين طول مستطيل وعرضه =

تعني إذا كان طول المستطيل = 3 سم فإن عرضه  = ......... . وفي المثلث أ ب جـ  القائم الزاوية في  ب

وهناك أربع نسب أخرى بين أطوال أضلاع هذا المثلث

يمكن أن تجد النسب التالية :

( يمكنك أن تجدها بنفسك إن أردت).   

                     

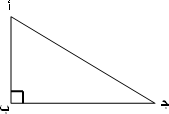سميت هذه النسب باسم النسب المثلثية لأنها تقارن بين أطوال أضلاع مثلث قائم الزاوية بالتحديد، ولكن هذه النسب ترتبط أيضا بزوايا المثلث ولهذا أعطاها علماء الرياضيات أسماءً مربوطة بزوايا المثلث كما سنتعرف تالياً.

1-

ارسم مثلثاً قائم الزاوية إحدى زواياه الحادة = 50 ْ.

كم مثلثاً يمكنك أن ترسم بحيث يحقق هذين الشرطين ؟

ارسم ثلاث مثلثات مختلفة تحقق هذين الشرطين ( كما في الشكل).

جـ = 50 ْ وطول الوتر أ جـ = 2 سم.		ليكن المثلث الأول أ ب جـ  قائم الزاوية في ب ، و
ع =50 ْ و طول الوتر س ع =4 سم.		وليكن المثلث الثاني س ص ع  قائم الزاوية في ص ، و
ﻫ = 50 ْ و طول الوتر و ﻫ = 5 سم .		وليكن المثلث الثالث و ل ﻫ  قائم الزاوية في ل ، و

     

 

    

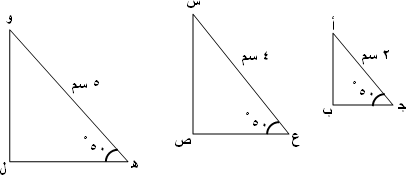
قس طول الضلع أ ب ( المقابل للزاوية 50 ْ ) في المثلث أ ب ﺠ  .اعمل جهدك أن تكون دقيقاً في قياساتك.

مقرباً لمنزلتين عشريتين.

جد النسبة

         

والنسبة

كرر الأمر  ذاته على المثلث س ص ع، والمثلث و ل ﻫ  وجد النسبة

إذا كان عملك دقيقاً فستجد أن  

      

بالطبع لن تكون النسب متساوية تماماً بل ستكون بينها فروق ولكن هذه الفروق ستكون طفيفة .

 

		وكذلك الحالة مع النسبة
	فهي ........... .	والامر ذاته مع النسبة

لقد لاحظت أنه على الرغم من اختلاف المثلثات الثلاث في أطوال أضلاعها فإن نسبة طول الضلع المقابل للزاوية50 ْ مقارنة بالوتر = مقداراً ثابتاً . ينطبق الأمر ذاته على الزوايا الأخرى .

جرب في نفس المثلثات إيجاد النسب

ستجدها متقاربة جداً وهي تمثل النسب الخاصة بالزاوية 40 ْ ( كيف عرفنا ؟) .

ولو رسمت مثلثات قائمة الزاوية أخرى بزوايا مختلفة ستجد دائماً

= مقداراً ثابتاً للزاوية المعنية .

أن نسبة

اتفق علماء الرياضيات منذ قرون على تسمية النسبة الناتجة عن حاصل قسمة :

). (	باسم جيب الزاوية ويرمز لها بالرمز (جا) أو

إذن جيب الزاوية هو عبارة عن نسبة بين طول الضلع المقابل لها إلى طول الوتر في نفس المثلث القائم الزاوية التي تكون هي إحدى زواياه ولهذا سميت نسبة مثلثية.

أمثلة :

مثال 1) :

س ص ع مثلث قائم الزاوية في ص ، فيه س ص = 5سم ، ص ع = 12سم

أوجد كلا من :   1) س ع ،     2) جا ع ،      3) جا س .

 الحل

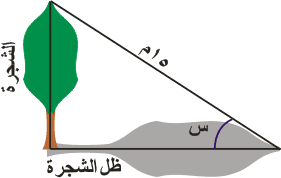
مثال 2):  في لحظة ما كانت المسافة بين قمة شجرة ورأس ظلها على سطح الارض تساوي 15م، وكان جاس = 0.6، جد ارتفاع الشجرة (مستعيناً بالشكل المجاور ) . الحل

مثال3) :

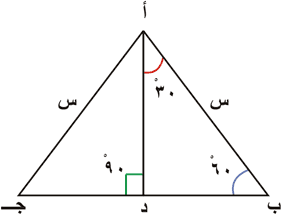يمثل الشكل المجاور مثلثاً متساوي الأضلاع، طول ضلعه س، أ د عمودي على الضلع ب ﺠ. اثبت أن جا 30 =

الحل

:

2-

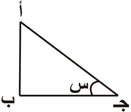هي النسبة المثلثية الأساسية الثانية وهي عبارة عن النسبة الناتجة عن قسمة طول الضلع المجاور للزاوية على طول وتر المثلث.في الشكل المجاور لقد رمزنا للزاوية القريبة من الرأس جـ بالرمز س ، والضلع المجاور لها هو الضلع ب جـ أما الوتر فهو أجـ ، إذن جيب تمام

تدريب :

ارجع إلى المثلثات التي رسمتها في موضوع جيب الزاوية، أوجد جيب تمام الزاوية 50 ْ في كل منها .

إذا كانت قياساتك صحيحة ستجد أن جيب تمام الزاوية 50 ْ= 0.60-0.64 تقريباً.

) .

يرمز لجيب تمام الزاوية بالرمز جتا أو (

أمثلة محلولة:-

مثال1:

أ ب جـ مثلث قائم الزاوية في ب ، فيه أ ب = 5 سم ، ب جـ = 12سم ، أ جـ =13 سم أوجد جتاجـ ، جتاأ.

الحل :

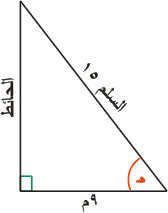
مثال 2: سلم طوله (15م) يستند إلى حائط، طرف السلم السفلي يبعد مقدار (9م) عن قاعدة الحائط، أوجد جيب تمام الزاوية بين السلم والأرض.    الحل :  جيب تمام الزاوية

مثال3:

يمثل الشكل المجاور  مثلثاً متساوي الأضلاع طول ضلعه س، أد عمودي على الضلع ب جـ ،

أثبت أن جتا30

الحل :

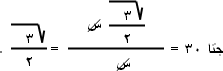
، هنا يجب أن نجد طول الضلع أ د لأنه هو الضلع المجاور للزاوية 30˚..

أثبت أن جتا=30

ملاحظة : لقد حسبنا طول أ د بدلالة س  في مثال (3) في موضوع الجيب .

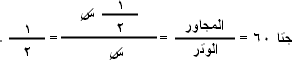
3-

النسبة المثلثية الأساسية الثالثة هي النسبة بين طول الضلع المقابل للزاوية وطول الضلع المجاور لها وتسمى ظل الزاوية .

قس بدقة طول كل من ضلعي القائمة في كل مثلث ثم أوجد ظا 50˚ بقسمة طول الضلع المقابل لها على الضلع المجاور لها.

إذا كانت قياساتك دقيقة ستجد أن ظل50 ْ ينحصر بين  1.19 ـ 1.29 . يرمزلظل الزاوية بالرمز ظا أو ظل .

مثال1) :

أبﺠ مثلث قائم الزاوية في ب، طول أ ب = 6سم ،  ب جـ = 8سم ،  ﺠ.  الحل : اوجد ظل

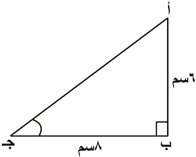سؤال : متى يكون ظل الزاوية يساوي 1 ؟   الجواب

سؤال مهم :

صحيحة؟ ولماذا . الجل:

؟ أو بالرموز ظاس =

هل هذه العلاقة ظل الزاوية =

مثال محلول :-

المثلث أب جـ قائم الزاوية في ب وأطوال أضلاعه. أ ب = 7 سم ، ب جـ = 24 سم ، أ جـ =25 سم أوجد النسب المثلثية للزاويتين أ ، جـ .

 الحل :       

                

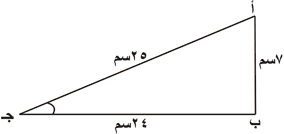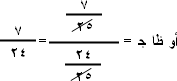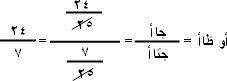للمناقشة :والآن سوف نتطرق إلى ثلاث نسب مثلثية تنتج عن قلب كل نسبة من النسب الأساسية الثلاث التي درسناها:       

1.قاطع الزاوية ويرمز له بالرمز قا وقاطع الزاوية

2.قاطع تمام الزاوية ويرمز له بالرمز قتا وقاطع تمام الزاوية

3.ظل تمام الزاوية ويرمز له بالرمز ظتا أو تطل وظل تمام الزاوية

 باختصار هناك ست نسب مثلثية والمثال التالي تدريب لكيفية إيجاد كل واحدة منها.

مثال محلول :- إذا كان أ ب جـ  مثلث قائم الزاوية في ب ، بحيث أ ب = 5سم ، ب جـ = 12سم ، أوجد النسب المثلثية الست للزاوية  أ ثم للزاوية جـ .

الحل : اولاً نرسم مثلث تقريبي  ثم نجد طول الوتر .

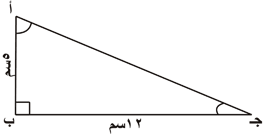ملاحظة :

الوتر في المثلث القائم الزاوية هو الضلع  المقابل للزاوية القائمة 90˚.

باستخدام نظرية  فيثاغورس

(الوتر)²=(الضلع₁)² +(الضلع₂)²

( أ جـ )² = (5)²+ (12)²

( أ جـ )²= 25 + 144

 ـ ( أ جـ )² = 169

= 13سم .

والآن نجد النسب المثلثية للزاوية (أ) وهي :

اما بالنسبة للزاوية (جـ)

أمثلة  :-

1) إذا كان جاس =، فما قيمة قتاس؟

2) إذا كان ظاس = 3 ، فما قيمة ظتاس ؟              

3) إذا كان قاس =7 ، فما قيمة جتاس؟